Orbes proporcionales para cúspides de las casas
Un planeta situado al final de una
casa pero muy cerca de la cúspide de la siguiente casa se considera como
si estuviese, de hecho, en la
casa próxima (se entiende que por hallarse en
conjunción a la cúspide). Por ejemplo, imaginemos que tenemos la cúspide
de la casa 3 a 28º de Aries y Júpiter se encuentra a 26º del mismo
signo; en tal caso, a efectos prácticos, tomamos a Júpiter en la casa 3 y
no en la 2 aunque se halla en una posición zodiacal anterior a la
cúspide.
Se establecen orbes de cierto número de grados para
las cúspides de las casas, operativos
no sólo para ubicar los planetas natales sino también para tránsitos.
Estos orbes se pueden variar de acuerdo a la cuadruplicidad de la casa
(angular, sucedente o cadente) tomando el máximo partido por los
ángulos. Por ejemplo, Charles Carter propone 10º para las cúspides de
casas angulares, 5º para las cadentes y un valor intermedio para las
sucedentes en su propio sistema de casas Poli-Ecuatorial (1).
En
astrología tradicional, la norma común es conceder un orbe general de 5
grados para todas las casas (2) aunque anteriormente se plantease para
los ángulos (3). Sin embargo esto choca con la idea clásica de que son
los planetas los que tienen su propio orbe y no los aspectos o las
cúspides. Otros autores como Stephen Arroyo han llegado a sugerir 6º de
orbe para todas las casas en el sistema de Koch (4).
Esta
regla, de otorgar 5 o 6 grados de orbe a las cúspides, puede parecer
adecuada en el sistema de casas iguales en el que cada casa tiene 30º,
pero nos genera un problema en los sistemas desiguales basados en
cuadrantes o
semi-arcos (Placidus, Koch, Topocéntrico, Alcabitius, etc...) ya
que esos 5º de
orbe pueden constituir la mitad de alguna casa en latitudes extremas,
resultando por tanto excesivos,
De manera que en los sistemas
de casas desiguales tenemos otra variable,
que es el tamaño de cada casa. Tomando como referencia un
sistema de casas iguales de 30º, 5º de orbe equivale al 16.67% de la
casa. Y aquí surge la pregunta ¿Qué ocurriría si mantuviésemos esa
misma
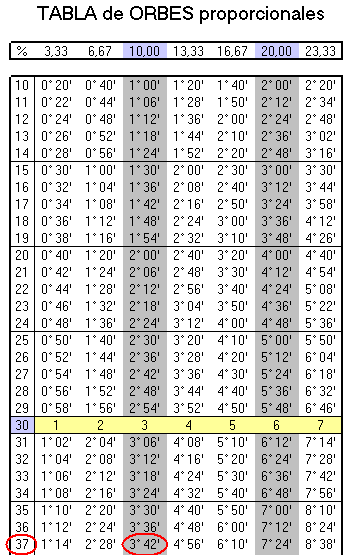
proporción en casas desiguales? El resultado lo podemos ver en la tabla
que presento a continuación. La idea es calcular una
serie de orbes proporcionales, para las cúspides de las casas, de
acuerdo al tamaño de las mismas.
Es muy sencilla de entender. En la columna de la izquierda tenemos
distintos valores correspondientes al tamaño de la casa en grados. En
las siete columnas adyacentes se calculan los orbes de acuerdo a las
proporciones de los grados marcados en la fila amarilla como referencia:
1º --- 3.33%
2º --- 6.67%
3º --- 10 %
4º --- 13.33 %
5º --- 16.67 %
6º --- 20 %
7º --- 23.33 %
Podemos elegir entre los valores de cualquiera de estas siete columnas a
conveniencia: de acuerdo a la importancia del planeta, su velocidad, o a
la cuadruplicidad de la casa.
Hay que precisar que aunque busquemos el orbe para la cúspide de la casa siguiente, el tamaño de la casa ha de corresponder a la precedente. De modo que si deseo obtener el orbe para la cúspide de 9, miraré en la primera columna el tamaño de la casa 8.
Resumiendo todo en un ejemplo. Supongamos que tenemos una casa 2 con un
tamaño de 37º y al final de la misma, cerca de la cúspide de la casa 3
hay algún planeta. Queremos determinar si tal planeta se puede incluir
en la 3 o sigue estando en la 2. Primero hemos de decidir qué orbe le
daríamos a la cúspide de la 3ª en casas iguales de 30º. Supongamos que
por ser Cadente acordamos 3º (si se tratara de una Luminaria podríamos
añadir algún grado extra). Entonces buscaríamos en la primera columna el
número 37 (tamaño de la casa 2) y de ahí, saltaríamos a la tercera
fila: 3º42'. Ese sería el orbe que le correspondería: vemos que aumenta
de 42' respecto a una casa de 30º porque se mantiene la proporción del
10% (indicado en la fila superior). Si en lugar de la casa 2, estamos
viendo la 3, podemos aumentar la proporción, ya que se trataría de un
ángulo (casa 4) y acudir a alguna de las columnas de la derecha.
Por supuesto, todo esto es totalmente teórico y al final la
elección de una u otra columna dependerá de muchos factores que pueden
ser, más o menos, subjetivos. Sin embargo me parece coherente tener en
cuenta las dimensiones domales a la hora de tomar este tipo de
decisiones y creo que la tabla puede ser de ayuda para experimentar de
forma organizada.
La tabla completa se puede descargar desde este link
ANEXO
Se me ha ocurrido una solución sencilla y más exacta que la anterior tabla, ya que estaremos basándonos en el propio cálculo del sistema de casas en cuestión grado-a-grado en lugar de casa por casa.
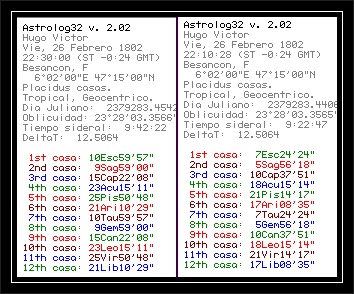
Se trata de tomar una tabla de casas o mediante la opción de "animar" la carta del software astrológico, y restarle al MC tantos grados como orbe vayamos a considerar (usualmente 5º).
Por ejemplo, en la siguiente carta el MC está a 23º15'Leo: al restarle 5º dejándolo a 18º15'Leo, las demás cúspides se recalculan automáticamente en tal proporción indicándonos los lugares exactos donde comienzan los orbes para cada casa. Podemos ir variando los grados a restar al MC según sea la casa angular, sucedente o cadente, si deseamos hacer tal distinción. El método es aplicable a cualquier sistema de casas.
El ascendente no se mueve a una velocidad constante sino que varía en
función ascensión del signo dependiendo de la latitud. Los signos de
corta ascensión tardan en ascender menos tiempo y producen casas más
largas. Los signos de larga ascensión tardan en ascender más tiempo y
producen casas más cortas.
Por esto pienso que es razonable
tomar el MC como referencia ya que su grado es la posición eclíptica de
la hora sideral
local expresada en términos de AR (ARMC, la Ascensión Recta del Medio
Cielo) para cualquier latitud. El MC avanza 1º en unos 3m56s, que es la
diferencia entre el día solar medio y el día sidéreo medio (23h56m4s).
Multiplicando 3m56s por los grados que deseemos para el orbe,
obtendremos la hora sideral a restar de la natal para recalcular las
cúspides de las casas. 19m40s para 5º.
Un truco para aplicar lo anterior de forma rápida es retrasar la fecha natal tantos días como grados
queramos haciendo clics en la opción de retroceder por días que suele
haber en muchos programas astrológicos. Por ejemplo, si queremos ver los
orbes de todas las cúspides correspondientes al sistema de casas que
tenemos seleccionado, hacemos 5 clics para retrasar 5 días la carta (con
la misma hora natal) y veremos que el Mc ha retrocedido aproximadamente
5º y las demás casas su proporción correspondiente.
Paris a.m.g.
Referencias
(1) Essays on the Foundations of Astrology. Charles E.O. Carter: Problems of the houses.
(2) The Rules of Chart Interpretation. (10). Rod Suskin.
(3) Guido Bonatti and His 146 Considerations (58).
http://www.renaissanceastrology.com/bonatti146considerations.html
(4) Astrology, Karma and Transformation: Inner Dimensions of the Birth Chart. Stephen Arroyo: Saturn: Its Nature & Cycles.
Añado una serie de artículos muy interesantes que recientemente ha escrito Anthony Louis acerca de este tema:
Does the 5-degree rule in horary make sense? by Anthony Louis – Astrology & Tarot Blog Link
The 5-degree rule in horary, part II by Anthony Louis – Astrology & Tarot Blog Link
The 5-degree Rule in Horary and the Twilight of the Gods (part III) by Anthony Louis – Astrology & Tarot Blog Link
Angular Diameter, Sect, the 5-degree rule and the Aries Ingress by Anthony Louis – Astrology & Tarot Blog Link